German Crystallographic Association ( DGK )
Study Group 16 (AK16): Aperiodic Crystals
Aperiodic crystals
Aperiodic crystals are crystals with an, in principle, perfect long-range order in the spatial arrangement of their atomic constituents. They are distinguished from the three-dimensional periodic crystals (the "normal" crystals in the classical sense) by just this fact, that their structures lack three-dimensional translational symmetry ( i.e. periodicity).
Three different kinds of aperiodic crystals are considered. It has however to be stressed, that these represent only borderline cases, the limits between them are not clearly defined but depend on the beholder and the applied structural model.
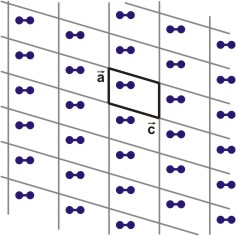
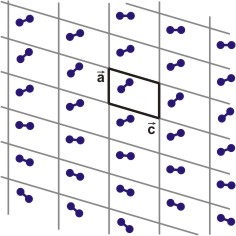
The structure of an incommensurately modulated crystal can be described with the aid of a so-called basic structure. This basic structure exhibits a three-dimensional space group symmetry, which is superposed by a periodic deformation, i.e. the modulation (in the example below it is an ordered rotation of the dumbbell about its respective centre of gravity). The periodicity of the modulation does not belong to the periodicity of the basic structure, what results in an modulated (aperiodic) structure.
|
|
||
| Periodic structure: The structure consists of a lattice and a dumbbell-like motif. It can be seen clearly, that the structure owns translational symmetry (periodicity) along the a-axis as well as along the c-axis. | Modulated structure: The motif was rotated about its respective centre of gravity, translational symmetry still exists but only along the c-axis. However, the rotation was not arbitrary but controlled, i.e. along the a-axis the structure still exhibits long-range order. |
The atomic parameter, i.e. fractional coordinates, occupancy and/or ADP, are given as the sum of the atomic parameter in the basic structure plus a deviation thereof (modulated structure = basic structure + modulation).
A composite crystal can be described as a coherent intergrowth of two (or more) modulated crystal structures. Its structure consists then of two (or more) subsystems, whose basic structures are mutually incommensurate. Each of the substructures has its own space-group symmetry. The space groups of the substructures can be uniquely derived from the overall superspace group.
The single lattices are not sublattices of a common (three-dimensional) one and it is not possible to express one lattice by the other one with rational numbers. These compounds do not possess one common basic lattice. As a consequence, one has for each subsystem one set of main reflections. Also the basic structures themselves are modulated due to the interaction between the subsystems. Nevertheless, the intergrowth is coherent, the composite crystals have to be considered as single thermodynamic phases.
The point symmetry of a quasicrystal is usually a non-crystallographic point group (crystal class), which is equivalent to an obligatory loss of the three-dimensional translational symmetry. Therefore, the quasicrystal can be characterized by the absence of an average Bravais lattice and/or the observation of "forbidden" crystallographic symmetry (i.e. a 5-, 10- or 12-fold rotation axis).
In contrast with modulated and composite crystals and because of the lack of a periodic basic structure, quasicrystals do not exhibit a clear lattice of main reflections. A simple distinction between main and satellite reflections is not possible.
The structural study of aperiodic crystals as well as the quantitative analysis of bond lengths, coordination spheres, and physical properties, requires methods which are different from those for periodic crystals. As example one might mention, that the symmetries of incommensurately modulated crystals and composite crystals can be described by so-called (3+d)-dimensional superspace groups, which are based on a three-dimensional crystallographic point-group and introduce additional dimensions to model the modulations of the structure.
___________________
March 2007